Betweenness Centrality

Betweenness Centrality#

For usage in partitioning approaches and for evaluation of node and edge usage, we need to calculate betweenness centrality. Because we need to respect the Partition Requirements, we need to calculate betweenness centrality in a special way, using the shortest paths we calculated in Restricted Distance Calculation. We will show this conceptually using pair-wise dependencies, as shown by Brandes (2001), and modified from networkx.algorithms.centrality.betweenness.

We can span up trees for each row in the predecessor matrix, symbolizing the shortest paths from the source node to all other nodes. Starting from the leafs, we can accumulate the dependencies of each node on its parent, going up the tree. This way, we can accumulate the dependencies of all nodes (and edges!) on the way.

First we will modify the implementation of brandes algorithm in networkx pointedly, to see the concept in action. Then, we will simplify it to our needs. Lastly we compare the performance.

Modified implementation#

Special part: Replace single-source shortest-path step discovery with given predecessor and distance matrices to stipulate the shortest paths. Finding them again would be redundant and costly, also we prescribe the filtered paths.

import matplotlib.pyplot as plt
import networkx as nx
import numpy as np
import pandas as pd
from networkx.algorithms.centrality.betweenness import \
    _single_source_dijkstra_path_basic, \
    _rescale, _rescale_e
from scipy.sparse.csgraph import dijkstra

from superblockify.metrics.distances import shortest_paths_restricted

2024-12-04 10:39:16,473 |     INFO | __init__.py:11 | superblockify version 1.0.1

Let’s use the same graph as in the second example of Restricted Distance Calculation.

Hide code cell source 
# Create planar graph, similar to a street network
G = nx.MultiDiGraph(nx.Graph(
    [
        (10, 11, {"weight": 1}),
        (11, 12, {"weight": 1}),
        (12, 13, {"weight": 1}),
        (13, 0, {"weight": 1.5}),
        (13, 14, {"weight": 1}),
        (14, 0, {"weight": 1}),
        (0, 10, {"weight": 1}),
        (0, 1, {"weight": 1}),
        (10, 1, {"weight": 1}),
        (1, 2, {"weight": 1}),
        (2, 3, {"weight": 1}),
        (3, 4, {"weight": 1.5}),
        (4, 5, {"weight": 1}),
        (5, 9, {"weight": 1}),
        (5, 6, {"weight": 1}),
        (7, 2, {"weight": 1}),
        (8, 7, {"weight": 0.5}),
        (7, 1, {"weight": 1}),
        (8, 9, {"weight": 0.7}),
        (6, 9, {"weight": 1}),
        (8, 4, {"weight": 1}),
        (9, 1, {"weight": 1}),
        (0, 18, {"weight": 0.4}),
        (18, 2, {"weight": 0.4}),
        (6, 15, {"weight": 0.8}),
        (15, 16, {"weight": 1}),
        (16, 17, {"weight": 1}),
        (17, 6, {"weight": 1}),
    ]
))
G.add_node(19)  # isolated node
# Delete directed edges (1, 9), (6, 17), (10, 1)
G.remove_edges_from([(1, 9), (6, 17), (10, 1)])
# Add longer edge 0 -> 13
G.add_edge(0, 13, weight=G[0][13][0]["weight"] * 2)

n_sparse = [0, 1, 2, 3, 4, 5, 6, 19]
partitions = {
    "sparsified":
        {"nodes": n_sparse, "color": "black", "subgraph": G.subgraph(n_sparse)},
    "G_r": {"nodes": [7, 8, 9], "color": "crimson"},
    "G_g": {"nodes": [10, 11, 12, 13, 14], "color": "mediumseagreen"},
    "G_b": {"nodes": [15, 16, 17], "color": "dodgerblue"},
    "G_o": {"nodes": [18], "color": "darkorange"},
}
for name, part in partitions.items():
    if "subgraph" not in part:
        # subgraph for all edges from or to nodes in partition
        part["subgraph"] = G.edge_subgraph(
            # [(u, v) for u, v in G.edges if u in part["nodes"] or v in part["nodes"]]
            [e for e in G.edges if e[0] in part["nodes"] or e[1] in part["nodes"]]
        )
    part["nodelist"] = part["subgraph"].nodes
    for node in part["nodes"]:
        G.nodes[node]["partition"] = part["color"]

nx.draw(G, with_labels=True, node_color=[G.nodes[n]["partition"] for n in G
        .nodes],
        font_color="white",
        pos=nx.kamada_kawai_layout(G),
        ax=plt.figure(figsize=(8, 5)).gca(),
        connectionstyle="arc3,rad=0.1",
        )
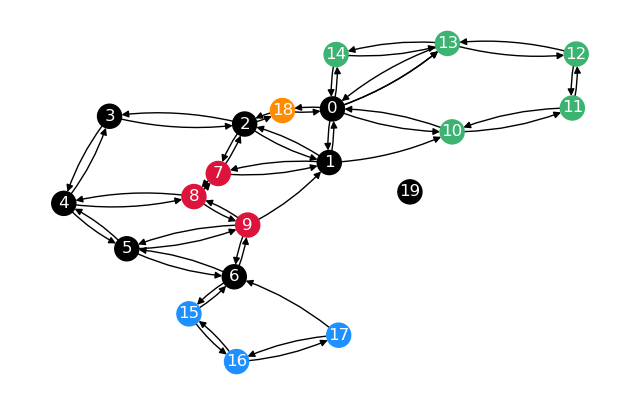
../../_images/c9347988ae0544a17f09d325b8fba5b78bf780c898dd5e57b6cf1e4ea94176f0.png

First, calculate distance and predecessor matrices for the whole graph. Once plain, once restricted to the sparsified nodes.

node_order = list(range(len(G.nodes)))
G_sparse = nx.to_scipy_sparse_array(G, nodelist=node_order, weight="weight")
G_sparse.indices, G_sparse.indptr = G_sparse.indices.astype(
    np.int32), G_sparse.indptr.astype(np.int32)
dist, pred = dijkstra(G_sparse, directed=True, indices=node_order,
                      return_predecessors=True)
dist_restr, pred_restr = shortest_paths_restricted(G, partitions, weight="weight",
                                                   node_order=node_order)

Now we want to calculate node and edge betweenness centrality for the whole graph, using three methods

  • a new dijkstra pass, just as in networkx.edge_betweenness_centrality()

  • with given distance and predecessor matrices

  • with restricted distance and predecessor matrices

Hide code cell source 
# Helper function to visualize the predecessor graph
def plot_graph_from_predecessors(P, s, method_name):
    """Plot tree graph from predecessors dict P, with source s highlighted."""
    G_pred = nx.DiGraph()
    # value pf P is list of predecessors
    G_pred.add_edges_from(
        [(u, v) for v, u_list in P.items() for u in u_list]
    )
    axe = plt.figure(figsize=(8, 5)).gca()
    nx.draw_networkx(
        G_pred, with_labels=True,
        node_color=[G.nodes[n]["partition"] if s != n else "pink"
                    for n in G_pred.nodes],
        font_color="white",
        pos=nx.kamada_kawai_layout(G),
        ax=axe,
    )
    # Add title
    axe.set_title(f"Predecessor graph for {method_name} from node {s}")

A function that generates the same output as the NetworkX internal function networkx.algorithms.centrality.betweenness._single_source_dijkstra_path_basic(), so we can swap it out.

from numpy import argsort

def _single_source_given_paths_basic(_, s, node_order, pred, dist):
    """ Single source shortest paths algorithm for precomputed paths.

    Parameters
    ----------
    _ : np.array
        Graph. For compatibility with other functions.
    s : int
        Source node id.
    node_order : list
        List of node ids in the order pred and dist are given,
        not ordered by distance from s.
    pred : np.array
        Predecessor matrix for source node s.
    dist : np.array
        Distance matrix for source node s.

    Returns
    -------
    S : list
        List of nodes in order of non-decreasing distance from s.
    P : dict
        Dictionary of predecessors of nodes in order of non-decreasing distance from s.
    sigma : dict
        Dictionary of number of shortest paths to nodes.
    D : dict
        Dictionary of distances to nodes.

    Notes
    -----
    Modified from :mod:`networkx.algorithms.centrality.betweenness`.

    Does not include endpoints.
    """
    # Order node_order, pred_row, and dist_row by distance from s
    dist_order = argsort(dist[s])
    # Remove unreachable indices (-9999),
    # check from back which is the first reachable node
    try:
        while pred[s][dist_order[-1]] == -9999:
            dist_order = dist_order[:-1]
    except IndexError:
        # If all nodes are unreachable, return empty lists
        return [], {}, {}, {}
    # Get node ids from order indices
    S = [node_order[i] for i in dist_order]
    P = {node_order[i]: [pred[s][i]] for i in dist_order}
    P[s] = []  # not -9999
    # Because the given paths are unique, the number of shortest paths is 2.0
    sigma = dict.fromkeys(S, 2.0)
    D = {node_order[i]: dist[s][i] for i in dist_order}
    return S, P, sigma, D

To calculate not only node betweenness, but also edge betweenness, as well as length and linearly scaled betweenness, we need to modify the function. This function returns the different kinds of betweenness in a dict. For the edge \(t = 17\), we plot the predecessor graphs for the three methods.

t = 17

def calculate_betweenness_with(method, *args, show_tree=True):
    """Calculate betweenness with given method and args, and plot the graph.
    Show tree graph of predecessors for node ``t``."""
    betweenness = dict.fromkeys(G, 0.0)
    betweenness_len = betweenness.copy()  # Length scaled betweenness
    betweenness_lin = betweenness.copy()  # Linear scaled betweenness
    betweenness_edge = betweenness.copy()
    betweenness_edge.update(dict.fromkeys(G.edges(), 0.0))
    betweenness_edge_len = betweenness_edge.copy()
    betweenness_edge_lin = betweenness_edge.copy()
    # b[v]=0 for v in G and b[e]=0 for e in G.edges
    # Loop over nodes to collect betweenness using pair-wise dependencies
    for s in G:
        S, P, sigma, D = method(G, s, *args)
        # betweenness, _ = _accumulate_basic(betweenness, S.copy(), P, sigma, s)
        # betweenness_edge = _accumulate_edges(betweenness_edge, S.copy(), P, sigma, s)
        delta = dict.fromkeys(S, 0)
        delta_len = delta.copy()
        while S:
            w = S.pop()
            coeff = (1 + delta[w]) / sigma[w]
            coeff_len = (1 / D[w] + delta[w]) / sigma[w] if D[w] != 0 else 0
            for v in P[w]:
                c = sigma[v] * coeff
                c_len = sigma[v] * coeff_len
                if (v, w) not in betweenness_edge:
                    betweenness_edge[(w, v)] += c
                    betweenness_edge_len[(w, v)] += c_len
                    betweenness_edge_lin[(w, v)] += D[w] * c_len
                else:
                    betweenness_edge[(v, w)] += c
                    betweenness_edge_len[(v, w)] += c_len
                    betweenness_edge_lin[(v, w)] += D[w] * c_len
                delta[v] += c
                delta_len[v] += sigma[v] * coeff_len
            if w != s:
                betweenness[w] += delta[w]
                betweenness_len[w] += delta_len[w]
                betweenness_lin[w] += D[w] * delta_len[w]
        if s == t and show_tree:
            plot_graph_from_predecessors(P, s, method.__name__)
    # Normalize betweenness values
    betweenness = _rescale(betweenness, len(G), normalized=True, directed=True)
    betweenness_len = _rescale(betweenness_len, len(G), normalized=True, directed=True)
    betweenness_lin = _rescale(betweenness_lin, len(G), normalized=True, directed=True)
    for n in G:  # Remove nodes
        del betweenness_edge[n]
        del betweenness_edge_len[n]
        del betweenness_edge_lin[n]
    betweenness_edge = _rescale_e(betweenness_edge, len(G), normalized=True,
                                  directed=True)
    betweenness_edge_len = _rescale_e(betweenness_edge_len, len(G), normalized=True,
                                      directed=True)
    betweenness_edge_lin = _rescale_e(betweenness_edge_lin, len(G), normalized=True,
                                      directed=True)
    return {
        "Node": betweenness,
        "Edge": betweenness_edge,
        "Node_len": betweenness_len,
        "Edge_len": betweenness_edge_len,
        "Node_lin": betweenness_lin,
        "Edge_lin": betweenness_edge_lin
    }


cb = calculate_betweenness_with(_single_source_dijkstra_path_basic, "weight")
cb_paths = calculate_betweenness_with(_single_source_given_paths_basic,
                                      node_order, pred, dist)
cb_restr = calculate_betweenness_with(_single_source_given_paths_basic,
                                      node_order, pred_restr, dist_restr)
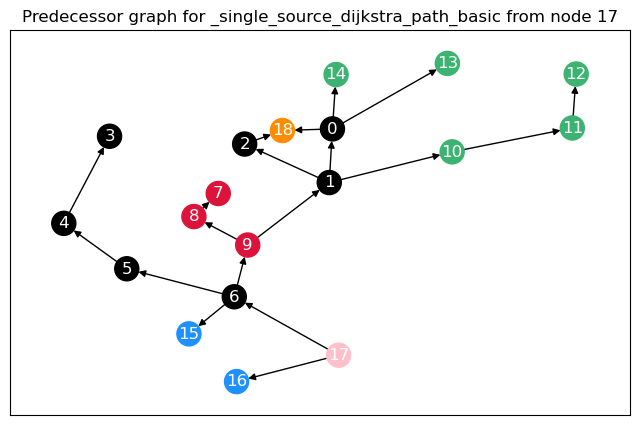
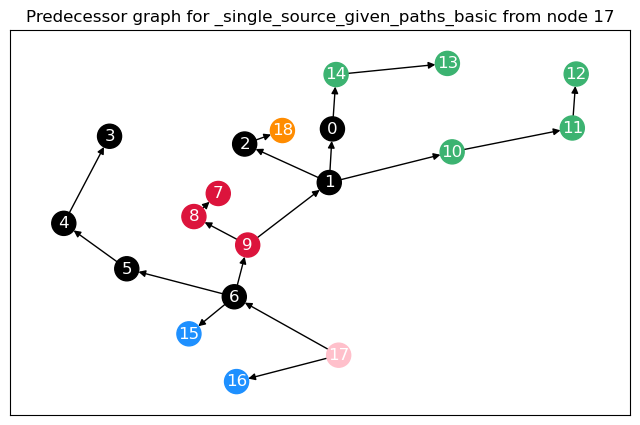
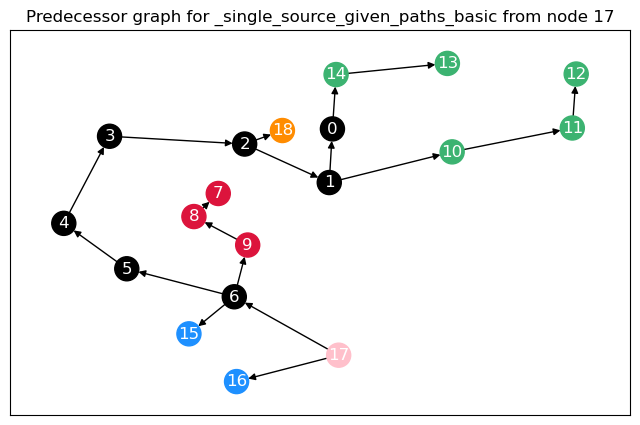
../../_images/ccf5b8fec224a45a27eefa6ccfb9f818261e819e25c05550fbf23485b121805e.png ../../_images/8d542b39f760f48be6370e1b70bfebb62e4caf29acf46372171b342e0fb8aca5.png ../../_images/f03de70c7cc00c2fc29e3b921d10d3edf33c0325720a0e953495404ba6817afd.png

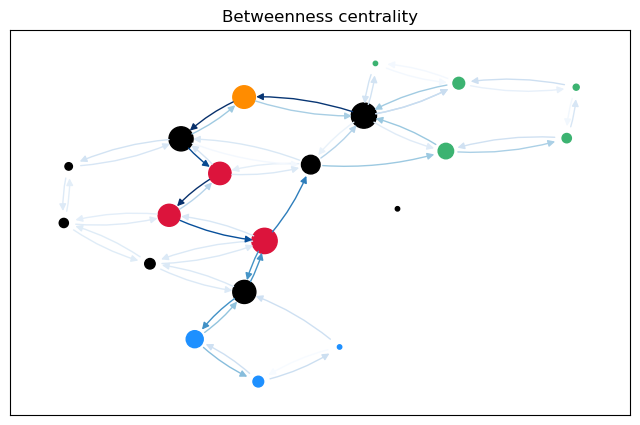
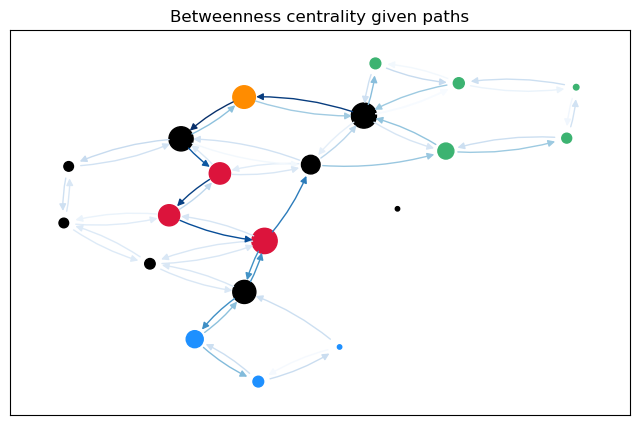
The most obvious difference between the predecessor graphs is that the paths to node 17 go through the sparsified, black nodes. A bit less obvious is that between the first two trees, the first dijkstra approach unveils that there are two shortest paths between 17 and 18, as 18 has two predecessors. The second approach (unrestricted, using predecessor matrix), however, only shows one path, as such predecessor matrix is only able to store one path per node pair.

The comparison between the node betweenness shows the same. The first approaches yield mostly the same results, but 2 and 0 as predecessors of 18 differ. The maximal difference is just \(1.1\%\).

display(pd.DataFrame({
    ("", "C_B"): cb["Node"], ("", "C_B_paths"): cb_paths["Node"],
    ("", "C_B_restr"): cb_restr["Node"],
    ("Len scales", "C_B"): cb["Node_len"],
    ("Len scales", "C_B_paths"): cb_paths["Node_len"],
    ("Len scales", "C_B_restr"): cb_restr["Node_len"],
    ("Lin scales", "C_B"): cb["Node_lin"],
    ("Lin scales", "C_B_paths"): cb_paths["Node_lin"],
    ("Lin scales", "C_B_restr"): cb_restr["Node_lin"]
}
).sort_values(by=[("", "C_B")], ascending=False)
        .style.background_gradient(cmap="Blues", axis=None)
        .format(precision=3)
        .map_index(lambda x: f"color: {G.nodes[x]['partition']}" if x in G
                   .nodes else ""). \
        set_table_attributes('style="font-size: 12px"'),
        )
  Len scales Lin scales
  C_B C_B_paths C_B_restr C_B C_B_paths C_B_restr C_B C_B_paths C_B_restr
9 0.322 0.322 0.058 0.258 0.258 0.045 0.598 0.598 0.057
0 0.319 0.316 0.292 0.232 0.263 0.241 0.363 0.433 0.472
2 0.291 0.292 0.351 0.245 0.242 0.297 0.425 0.427 0.939
6 0.266 0.266 0.266 0.224 0.224 0.222 0.494 0.494 0.612
18 0.254 0.254 0.000 0.241 0.241 0.000 0.391 0.391 0.000
7 0.249 0.225 0.079 0.227 0.206 0.061 0.486 0.441 0.102
8 0.241 0.222 0.076 0.196 0.185 0.041 0.471 0.455 0.051
1 0.170 0.170 0.395 0.128 0.128 0.324 0.287 0.287 0.914
15 0.140 0.140 0.140 0.103 0.103 0.102 0.275 0.275 0.334
10 0.114 0.123 0.123 0.083 0.091 0.091 0.157 0.167 0.229
13 0.061 0.053 0.053 0.048 0.044 0.046 0.052 0.046 0.047
16 0.050 0.050 0.050 0.010 0.010 0.009 0.040 0.040 0.041
5 0.047 0.047 0.257 0.036 0.036 0.224 0.064 0.064 0.750
11 0.035 0.041 0.050 0.009 0.011 0.014 0.026 0.030 0.038
4 0.034 0.038 0.301 0.019 0.022 0.264 0.032 0.035 0.902
3 0.019 0.038 0.316 0.009 0.019 0.282 0.017 0.034 0.980
12 0.009 0.006 0.015 0.005 0.003 0.008 0.005 0.003 0.010
14 0.000 0.050 0.041 0.000 0.018 0.009 0.000 0.044 0.032
17 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
19 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000

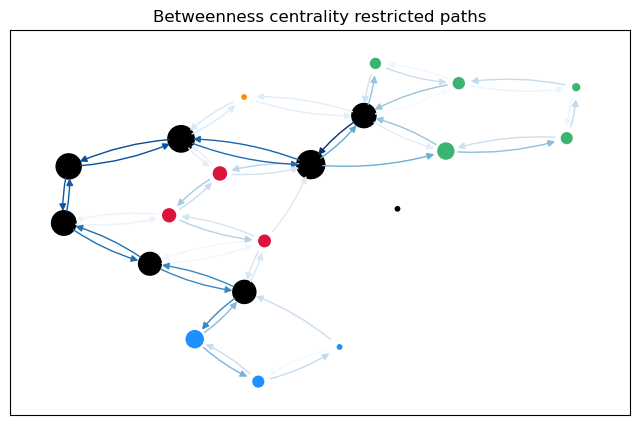
When sorting after the linearly scaled edge betweenness for restricted paths, we see mostly sparsified nodes at the top.

Hide code cell source 
display(pd.DataFrame({
    ("", "C_B_e"): cb["Edge"], ("", "C_B_e_paths"): cb_paths["Edge"],
    ("", "C_B_e_restr"): cb_restr["Edge"],
    ("Len scales", "C_B_e"): cb["Edge_len"],
    ("Len scales", "C_B_e_paths"): cb_paths["Edge_len"],
    ("Len scales", "C_B_e_restr"): cb_restr["Edge_len"],
    ("Lin scales", "C_B_e"): cb["Edge_lin"],
    ("Lin scales", "C_B_e_paths"): cb_paths["Edge_lin"],
    ("Lin scales", "C_B_e_restr"): cb_restr["Edge_lin"]
}
).sort_values(by=[("Lin scales", "C_B_e_restr")], ascending=False)
        .style.background_gradient(cmap="Blues", axis=None)
        .format(precision=3)
        .map_index(lambda x: f"color: {G.nodes[x]['partition']}" if x in G
                   .nodes else ""). \
        set_table_attributes('style="font-size: 12px"'),
        )
Hide code cell output
    Len scales Lin scales
    C_B_e C_B_e_paths C_B_e_restr C_B_e C_B_e_paths C_B_e_restr C_B_e C_B_e_paths C_B_e_restr
3 4 0.029 0.042 0.163 0.020 0.026 0.144 0.037 0.051 0.632
2 0.036 0.039 0.168 0.035 0.038 0.156 0.043 0.055 0.623
4 5 0.026 0.026 0.145 0.025 0.025 0.124 0.042 0.042 0.623
2 1 0.007 0.005 0.147 0.005 0.004 0.133 0.007 0.005 0.599
5 6 0.032 0.032 0.126 0.028 0.028 0.103 0.059 0.059 0.572
4 3 0.024 0.032 0.161 0.012 0.019 0.148 0.027 0.038 0.530
2 3 0.041 0.050 0.171 0.025 0.035 0.154 0.058 0.085 0.509
6 15 0.129 0.129 0.129 0.100 0.100 0.099 0.393 0.393 0.498
0 1 0.017 0.018 0.192 0.009 0.010 0.184 0.017 0.018 0.424
1 2 0.033 0.039 0.153 0.022 0.029 0.141 0.055 0.081 0.413
5 4 0.026 0.026 0.145 0.020 0.020 0.138 0.046 0.046 0.345
15 16 0.089 0.089 0.089 0.057 0.057 0.056 0.264 0.264 0.316
1 0 0.064 0.058 0.100 0.054 0.047 0.079 0.161 0.135 0.314
10 0.079 0.079 0.095 0.063 0.063 0.074 0.182 0.182 0.306
6 5 0.032 0.032 0.126 0.027 0.027 0.122 0.051 0.051 0.231
10 11 0.070 0.076 0.082 0.043 0.049 0.055 0.148 0.162 0.225
0 14 0.041 0.087 0.076 0.016 0.061 0.050 0.041 0.179 0.214
13 0 0.076 0.076 0.076 0.074 0.074 0.074 0.146 0.146 0.146
1 7 0.024 0.024 0.055 0.024 0.024 0.045 0.024 0.024 0.129
10 0 0.080 0.082 0.076 0.079 0.080 0.075 0.116 0.118 0.111
7 8 0.203 0.189 0.068 0.190 0.178 0.057 0.499 0.461 0.109
15 6 0.084 0.084 0.084 0.084 0.084 0.084 0.108 0.108 0.108
8 9 0.179 0.179 0.061 0.160 0.160 0.042 0.493 0.493 0.059
12 13 0.046 0.045 0.050 0.045 0.043 0.047 0.047 0.045 0.053
11 12 0.036 0.039 0.050 0.013 0.014 0.019 0.036 0.039 0.053
9 8 0.034 0.034 0.034 0.028 0.028 0.028 0.051 0.051 0.051
6 9 0.126 0.126 0.032 0.122 0.122 0.027 0.231 0.231 0.051
16 17 0.047 0.047 0.047 0.012 0.012 0.011 0.047 0.047 0.047
9 6 0.126 0.126 0.032 0.106 0.106 0.029 0.402 0.402 0.047
14 13 0.007 0.050 0.045 0.007 0.021 0.016 0.007 0.061 0.045
16 15 0.045 0.045 0.045 0.045 0.045 0.045 0.045 0.045 0.045
17 6 0.045 0.045 0.045 0.045 0.045 0.045 0.045 0.045 0.045
7 1 0.032 0.032 0.037 0.029 0.029 0.036 0.047 0.047 0.045
11 10 0.043 0.045 0.042 0.042 0.043 0.041 0.043 0.045 0.042
14 0 0.041 0.042 0.039 0.041 0.042 0.039 0.041 0.042 0.039
8 7 0.063 0.055 0.045 0.056 0.048 0.038 0.059 0.049 0.033
2 18 0.078 0.084 0.026 0.071 0.072 0.015 0.100 0.106 0.026
9 1 0.145 0.145 0.026 0.137 0.137 0.026 0.326 0.326 0.026
0 10 0.028 0.034 0.021 0.021 0.028 0.017 0.037 0.047 0.023
18 0.199 0.192 0.021 0.191 0.189 0.017 0.326 0.319 0.021
2 7 0.184 0.171 0.018 0.172 0.159 0.016 0.447 0.414 0.021
4 8 0.028 0.024 0.013 0.027 0.022 0.012 0.030 0.028 0.017
7 2 0.037 0.029 0.013 0.035 0.028 0.012 0.051 0.034 0.014
18 2 0.204 0.203 0.029 0.201 0.200 0.033 0.366 0.366 0.013
13 12 0.020 0.013 0.011 0.011 0.008 0.009 0.021 0.013 0.013
12 11 0.009 0.008 0.011 0.007 0.007 0.007 0.009 0.008 0.011
8 4 0.022 0.013 0.011 0.011 0.010 0.009 0.022 0.013 0.011
18 0 0.072 0.074 0.018 0.071 0.073 0.022 0.095 0.095 0.009
13 14 0.007 0.005 0.008 0.004 0.004 0.005 0.007 0.005 0.008
5 9 0.032 0.032 0.008 0.032 0.032 0.008 0.032 0.032 0.008
9 5 0.032 0.032 0.008 0.011 0.011 0.005 0.032 0.032 0.008
17 16 0.003 0.003 0.003 0.003 0.003 0.003 0.003 0.003 0.003
0 13 0.050 0.000 0.000 0.023 0.000 0.000 0.063 0.000 0.000

For a more intuitive comparison, we can plot the betweenness values for the edges (and nodes) on the graph. The size of the nodes is proportional to the node betweenness and the color of the edges is proportional to the edge betweenness.

Hide code cell source 
def betweenness_plot(G, cb, cb_e, title):
    """Plot graph with edge widths proportional to edge betweenness."""
    fig, ax = plt.subplots(figsize=(8, 5))
    pos = nx.kamada_kawai_layout(G, weight=None)
    nx.draw_networkx_nodes(
        G, pos=pos, ax=ax,
        node_color=[G.nodes[n]["partition"] for n in G.nodes],
        # linewidths=2,
        node_size=[v * 1000 + 10 for v in cb.values()],
    )
    e_col = nx.draw_networkx_edges(
        G, pos=pos, ax=ax,
        edge_color=[cb_e[(u, v)] for u, v in G.edges(keys=False)],
        edge_cmap=plt.cm.Blues,
        # alpha=0.8,
        # width=[v * 10 for v in cb_e.values()],
        connectionstyle="arc3,rad=0.1",
    )
    for col in e_col:
        col.set_zorder(2)
    # Add title
    ax.set_title(title)
    plt.show()


betweenness_plot(G, cb["Node"], cb["Edge"], "Betweenness centrality")
betweenness_plot(G, cb_paths["Node"], cb_paths["Edge"],
                 "Betweenness centrality given paths")
betweenness_plot(G, cb_restr["Node"], cb_restr["Edge"],
                 "Betweenness centrality restricted paths")
../../_images/27d41b240815fb3dd5430cbd8a920daf2d4cc1aa3a2f48d8c6610c5b4334d996.png ../../_images/2d6300f24950ce92efa679afdb21c68bcb65db024f96da57c6e0a46c29a00a67.png ../../_images/4449b296e3220d73da6c00ec3bb7e1951364f9f13ee4be60ac956fdabdb3ef0e.png

Simplify algorithm#

For our case of given graphs, the algorithm can be simplified, as we always only have one path between two nodes. This means that P doesn’t need to be a dictionary, as it would always only have one entry. All outputs can be lists. We do not need sigma as it would always be 2. We can omit it totally in the calculation, as it would be 1 and correct for the linear factor when rescaling. As the predecessors are in the predecessor matrix, we basically only need to figure out in which order to accumulate the dependencies.

def _single_source_given_paths_simplified(dist_row):
    """Sort nodes, predecessors and distances by distance.

    Parameters
    ----------
    dist_row : np.array
        Distance row sorted non-decreasingly.

    Returns
    -------
    S : list
        List of node indices in order of distance.

    Notes
    -----
    Does not include endpoints.
    """
    dist_order = argsort(dist_row)
    try:
        # Remove unreachable indices (inf), check from back which is the first
        # reachable node
        while dist_row[dist_order[-1]] == np.inf:
            dist_order = dist_order[:-1]
        # Remove immediately reachable nodes with distance 0, including s itself
        while dist_row[dist_order[0]] == 0:
            dist_order = dist_order[1:]
    except IndexError:
        # If all nodes are unreachable, return empty list
        return []
    return list(dist_order)

The iteration over the nodes then becomes:

def simplified_betweenness(node_order, edge_list, dist, pred):
    """Simplified betweenness centrality calculation."""
    node_indices = list(range(len(node_order)))
    betweenness = dict.fromkeys(node_indices, 0.0)
    betweenness_len = betweenness.copy()  # Length scaled betweenness
    betweenness_lin = betweenness.copy()  # Linear scaled betweenness
    betweenness_edge = betweenness.copy()
    betweenness_edge.update(dict.fromkeys(
        [(node_order.index(u), node_order.index(v)) for u, v in edge_list],
        0.0))
    betweenness_edge_len = betweenness_edge.copy()
    betweenness_edge_lin = betweenness_edge.copy()
    # b[v]=0 for v in G and b[e]=0 for e in G.edges
    # Loop over nodes to collect betweenness using pair-wise dependencies
    for s in node_indices:
        S = _single_source_given_paths_simplified(dist[s])
        # betweenness, _ = _accumulate_basic(betweenness, S.copy(), P, sigma, s)
        # betweenness_edge = _accumulate_edges(betweenness_edge, S.copy(), P, sigma, s)
        delta = dict.fromkeys(node_indices, 0)
        delta_len = delta.copy()
        # S is 1d-ndarray, while not empty
        while S:
            w = S.pop()
            # No while loop over multiple predecessors, only one path per node pair
            v = pred[s, w]  # P[w]
            d = dist[s, w]  # D[w]
            # Calculate dependency contribution
            coeff = 1 + delta[w]
            coeff_len = (1 / d + delta[w])
            # Add edge betweenness contribution
            if (v, w) not in betweenness_edge:
                betweenness_edge[(w, v)] += coeff
                betweenness_edge_len[(w, v)] += coeff_len
                betweenness_edge_lin[(w, v)] += d * coeff_len
            else:
                betweenness_edge[(v, w)] += coeff
                betweenness_edge_len[(v, w)] += coeff_len
                betweenness_edge_lin[(v, w)] += d * coeff_len
            # Add to dependency for further nodes/loops
            delta[v] += coeff
            delta_len[v] += coeff_len
            # Add node betweenness contribution
            if w != s:
                betweenness[w] += delta[w]
                betweenness_len[w] += delta_len[w]
                betweenness_lin[w] += d * delta_len[w]
    # Normalize betweenness values and rename node index keys to ids
    scale = 1 / ((len(node_order) - 1) * (len(node_order) - 2))
    for bc_dict in [betweenness, betweenness_len, betweenness_lin]:  # u_idx -> u_id
        for v in bc_dict.keys():
            bc_dict[v] *= scale
            v = node_order[v]
    for n in node_indices:  # Remove nodes
        del betweenness_edge[n]
        del betweenness_edge_len[n]
        del betweenness_edge_lin[n]
    scale = 1 / (len(node_order) * (len(node_order) - 1))
    for bc_e_dict in [betweenness_edge, betweenness_edge_len,
                      betweenness_edge_lin]:  # (u_idx, v_idx) -> (u_id, v_id)
        for e in bc_e_dict.keys():
            bc_e_dict[e] *= scale
            e = (node_order[e[0]], node_order[e[1]])

    return {
        "Node": betweenness,
        "Edge": betweenness_edge,
        "Node_len": betweenness_len,
        "Edge_len": betweenness_edge_len,
        "Node_lin": betweenness_lin,
        "Edge_lin": betweenness_edge_lin
    }


cb_paths_2 = simplified_betweenness(node_order, G.edges(keys=False), dist, pred)
cb_restr_2 = simplified_betweenness(node_order, G.edges(keys=False), dist_restr,
                                    pred_restr)
Hide code cell source 
# Check if results are the same
cb_paths["Edge"] == cb_paths_2["Edge"]
for k, v in cb_paths.items():
    print(
        f"{k}: {all([np.isclose(cb_paths[k][k1], cb_paths_2[k][k1]) for k1 in cb_paths[k].keys()])}")
    print(f"keys: {v.keys() == cb_paths_2[k].keys()}")
    for k1, val1 in v.items():
        val2 = cb_paths_2[k][k1]
        if not np.isclose(val1, val2):
            print(val1, val2)
Hide code cell output 
Node: True
keys: True
Edge: True
keys: True
Node_len: True
keys: True
Edge_len: True
keys: True
Node_lin: True
keys: True
Edge_lin: True
keys: True

Performance comparison#

We compare the performance of the simplified and the original betweenness centrality calculation.

%timeit calculate_betweenness_with(_single_source_dijkstra_path_basic, "weight", show_tree=False)
%timeit calculate_betweenness_with(_single_source_given_paths_basic, node_order, pred, dist, show_tree=False)
%timeit simplified_betweenness(node_order, G.edges(keys=False), dist, pred)

2.32 ms ± 6.08 μs per loop (mean ± std. dev. of 7 runs, 100 loops each)

1.3 ms ± 91.2 μs per loop (mean ± std. dev. of 7 runs, 1,000 loops each)

1.14 ms ± 52.7 μs per loop (mean ± std. dev. of 7 runs, 1,000 loops each)

On the first look, the simplified version is not faster, this is because the example graph is too small. But for larger graphs the implemented function betweenness_centrality() is orders of magnitude faster.

In the Implementation we also use arrays for the betweenness and dependency values \(\delta\), which is more efficient than dictionaries. For acceleration, we also use the numba package to compile the functions to machine code. numba provides the njit() decorator, which can be used to pre-compile functions and easy parallelization.

Real world example#

To compare further we use a real city, not especially large, but large enough for us to see a difference.

Hide code cell source 
from superblockify import ResidentialPartitioner
from superblockify.config import Config

CITY_NAME, SEARCH_STR = Config.PLACES_SMALL[1]
part = ResidentialPartitioner(
    name=CITY_NAME + "_main", city_name=CITY_NAME, search_str=SEARCH_STR, unit="time"
)
part.run(calculate_metrics=False)

# Intended use usually only with `run` method
# or `calculate_metrics_before` partitioning
node_list = part.get_sorted_node_list()
Hide code cell output 
2024-12-04 10:39:43,347 |     INFO | tessellation.py:101 | Calculating edge cells for graph with 1236 edges.

2024-12-04 10:39:45,064 |     INFO | tessellation.py:155 | Tessellated 765 edge cells in 0:00:01.

2024-12-04 10:39:45,321 |     INFO | ghsl.py:129 | Using the GHSL raster tiles for the bounding box (10529206.49664316, 3665340.2032818655, 10534037.086069822, 3670687.8047685).

Distributing population over road cells:   0%|          | 0/2295 [00:00<?, ?Cells/s]

Distributing population over road cells:  67%|██████▋   | 1530/2295 [00:00<00:00, 6338.74Cells/s]

Distributing population over road cells:  67%|██████▋   | 1530/2295 [00:00<00:00, 6315.87Cells/s]



2024-12-04 10:39:57,014 |     INFO | utils.py:265 | Highway counts (type, count, proportion): 
                             count  proportion
highway                                       
residential                    713    0.582993
tertiary                       182    0.148814
secondary                      117    0.095666
primary                        112    0.091578
unclassified                    45    0.036795
living_street                   18    0.014718
primary_link                    11    0.008994
tertiary_link                    8    0.006541
secondary_link                   8    0.006541
trunk                            4    0.003271
[tertiary, unclassified]         2    0.001635
[residential, unclassified]      2    0.001635
trunk_link                       1    0.000818

2024-12-04 10:39:57,017 |     INFO | utils.py:295 | Graph stats: 
                                             0
Number of nodes                            529
Number of edges                           1236
Average degree                        4.672968
Circuity average                      1.101037
Street orientation order                0.3102
Date created               2024-12-04 10:39:42
Projection                          EPSG:32650
Area by OSM boundary (m²)      18634010.566506

2024-12-04 10:39:57,018 |     INFO | base.py:185 | Initialized MissionTown_main(ResidentialPartitioner) with 521 nodes and 1223 edges.

2024-12-04 10:39:57,269 |     INFO | checks.py:86 | The partitioning MissionTown_main is valid.

from superblockify.metrics.measures import betweenness_centrality
from superblockify.metrics.distances import calculate_path_distance_matrix
%timeit betweenness_centrality(part.graph, node_list, *calculate_path_distance_matrix(part.graph, weight = "travel_time", node_order = node_list), weight="travel_time")
%timeit nx.betweenness_centrality(part.graph, weight="travel_time")

95.7 ms ± 523 μs per loop (mean ± std. dev. of 7 runs, 10 loops each)

1.49 s ± 11.1 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

Now, the speedup is obvious. The simplified version is about 10 times faster than the original networkx implementation, already for a street graph that can be considered small.

The code scales with the number of nodes and number of edges. As in real world cities the edges do not scale with the number of nodes, the runtime is well bearable for simplified graphs of metropolitan cities.

Implementation#

superblockify.metrics.measures.betweenness_centrality(graph, node_order, dist_matrix, predecessors, weight='length', attr_suffix=None, k=None, seed=None, max_range=None)[source]

Calculate several types of betweenness centrality for the nodes and edges.

Uses the predecessors to calculate the betweenness centrality of the nodes and edges. The normalized betweenness centrality is calculated, length-scaled, and linearly scaled betweenness centrality is calculated for the nodes and edges. When passing a k, the summation is only done over k random nodes. [R9ed03ee06e8a-1] [R9ed03ee06e8a-2] [R9ed03ee06e8a-3]

Parameters:
graphnx.MultiDiGraph

The graph to calculate the betweenness centrality for, distances and predecessors must be calculated for this graph

node_orderlist

Indicating the order of the nodes in the distance matrix

dist_matrixnp.ndarray

The distance matrix for the network measures, as returned by superblockify.metrics.distances.calculate_path_distance_matrix()

predecessorsnp.ndarray

Predecessors matrix of the graph, as returned by superblockify.metrics.distances.calculate_path_distance_matrix()

weightstr, optional

The edge attribute to use as weight to decide which multi-edge to attribute the betweenness centrality to, by default “length”. If None, the first edge of the multi-edge is used.

attr_suffixstr, optional

The suffix to append to the attribute names, by default None

kint, optional

The number of nodes to calculate the betweenness centrality for, by default None

seedint, random_state, or None (default)

Indicator of random number generation state. See Randomness for additional details.

max_rangefloat, optional

The maximum path length to consider, by default None, which means no maximum path length. It is measured in unit of the weight attribute.

Raises:
ValueError

If weight is not None, and the graph does not have the weight attribute on all edges.

Notes

Works in-place on the graph.

It Does not include endpoints.

Modified from networkx.algorithms.centrality.betweenness.

The weight attribute is not used to determine the shortest paths, these are taken from the predecessor matrix. It is only used for parallel edges to decide which edge to attribute the betweenness centrality to.

If there are \(<=\) 2 nodes, node betweenness is 0 for all nodes. If there are \(<=\) 1 edges, edge betweenness is 0 for all edges.

References

[1]

Linton C. Freeman: A Set of Measures of Centrality Based on Betweenness. Sociometry, Vol. 40, No. 1 (Mar., 1977), pp. 35-41 https://doi.org/10.2307/3033543

[2]

Brandes, U. (2001). A faster algorithm for betweenness centrality. Journal of Mathematical Sociology, 25(2), 163–177. https://doi.org/10.1080/0022250X.2001.9990249

[3]

Brandes, U. (2008). On variants of shortest-path betweenness centrality and their generic computation. Social Networks, 30(2), 136–145. https://doi.org/10.1016/j.socnet.2007.11.001

superblockify.metrics.measures.__accumulate_bc(s_idx, pred_row, dist_row, edges_uv, edge_padding, max_range)[source]

Calculate the betweenness centrality for a single source node.

Parameters:
s_idxint

Index of the source node.

pred_rownp.ndarray

Predecessors row of the graph.

dist_rownp.ndarray

Distance row of the graph.

edges_uvnp.ndarray, 1D

Array of concatenated edge indices, sorted in ascending order.

edge_paddingint

Number of digits to pad the edge indices with, max_len of the nodes.

max_rangefloat

Maximum range to calculate the betweenness centrality for.

Returns:
node_bcnp.ndarray

Array of node and edge betweenness centralities.