Street Tessellation#
In this notebook we show how the street tesselation is working and some of the process how we got there. See Implementation for a usage example and the function stubs. How the population is distributed is explained in the next notebook Street Population Density.
Show code cell source
import geopandas as gpd
import matplotlib.pyplot as plt
import osmnx as ox
import shapely as shp
import superblockify as sb
from superblockify.config import logger, Config
2024-12-04 10:42:03,306 | INFO | __init__.py:11 | superblockify version 1.0.1
First we will get a partitioned city, namely Scheveningen. We can do this easily with
a superblockify partitioner.
Show code cell source
CITY_NAME, SEARCH_STR = Config.PLACES_SMALL[2]
logger.info(
"Running partitioner for %s with search string %s.", CITY_NAME, SEARCH_STR
)
part = sb.ResidentialPartitioner(
name=CITY_NAME + "_main", city_name=CITY_NAME, search_str=SEARCH_STR
)
part.run(calculate_metrics=False, make_plots=True)
Show code cell output
2024-12-04 10:42:03,311 | INFO | 351138818.py:2 | Running partitioner for Scheveningen with search string Scheveningen, The Hague, Netherlands.
2024-12-04 10:42:09,528 | INFO | tessellation.py:101 | Calculating edge cells for graph with 2303 edges.
2024-12-04 10:42:11,507 | INFO | tessellation.py:155 | Tessellated 1551 edge cells in 0:00:01.
2024-12-04 10:42:11,800 | INFO | ghsl.py:129 | Using the GHSL raster tiles for the bounding box (314241.7133448336, 6089247.811732536, 318634.9651467116, 6093522.611401822).
Distributing population over road cells: 0%| | 0/1551 [00:00<?, ?Cells/s]
Distributing population over road cells: 3102Cells [00:00, 12257.99Cells/s]
Distributing population over road cells: 3102Cells [00:00, 12205.85Cells/s]
2024-12-04 10:42:15,659 | INFO | utils.py:265 | Highway counts (type, count, proportion):
count proportion
highway
residential 1833 0.800087
secondary 253 0.110432
tertiary 111 0.048450
living_street 63 0.027499
unclassified 24 0.010476
[residential, unclassified] 5 0.002182
secondary_link 1 0.000436
trunk 1 0.000436
2024-12-04 10:42:15,662 | INFO | utils.py:295 | Graph stats:
0
Number of nodes 996
Number of edges 2303
Average degree 4.624498
Circuity average 1.040085
Street orientation order 0.077344
Date created 2024-12-04 10:42:08
Projection EPSG:32631
Area by OSM boundary (m²) 14543814.359886
2024-12-04 10:42:15,663 | INFO | base.py:185 | Initialized Scheveningen_main(ResidentialPartitioner) with 986 nodes and 2291 edges.
2024-12-04 10:42:16,075 | INFO | checks.py:86 | The partitioning Scheveningen_main is valid.
2024-12-04 10:42:16,075 | INFO | plot.py:42 | Plotting partitions graph for Scheveningen_main with attribute `residential`
/home/runner/micromamba/envs/sb_env/lib/python3.12/site-packages/osmnx/plot.py:261: UserWarning: *c* argument looks like a single numeric RGB or RGBA sequence, which should be avoided as value-mapping will have precedence in case its length matches with *x* & *y*. Please use the *color* keyword-argument or provide a 2D array with a single row if you intend to specify the same RGB or RGBA value for all points.
ax.scatter( # type: ignore[union-attr]
2024-12-04 10:42:16,569 | INFO | plot.py:230 | Plotting component size rank for Scheveningen_main with attribute `residential`
2024-12-04 10:42:16,875 | INFO | plot.py:95 | Plotting component graph for Scheveningen_main with attribute `residential`
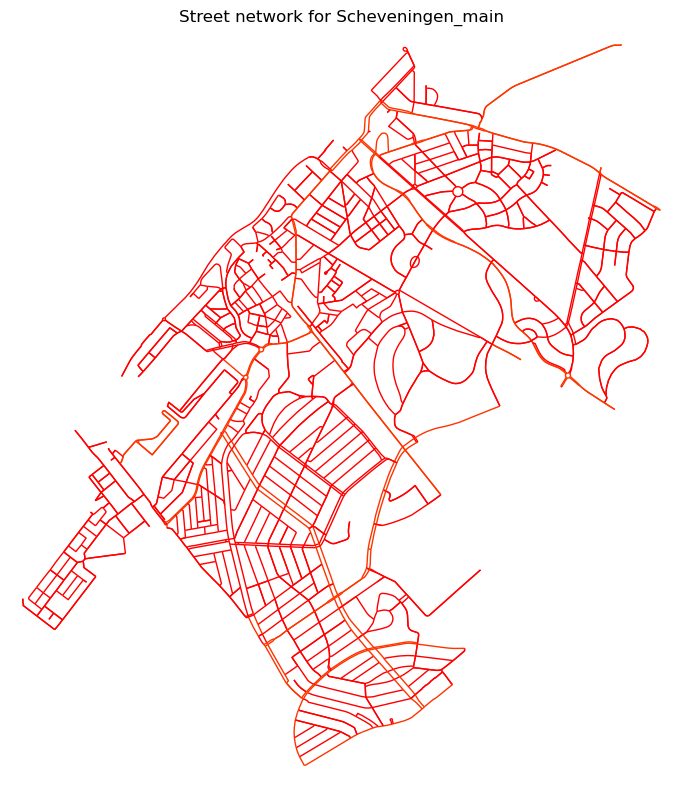
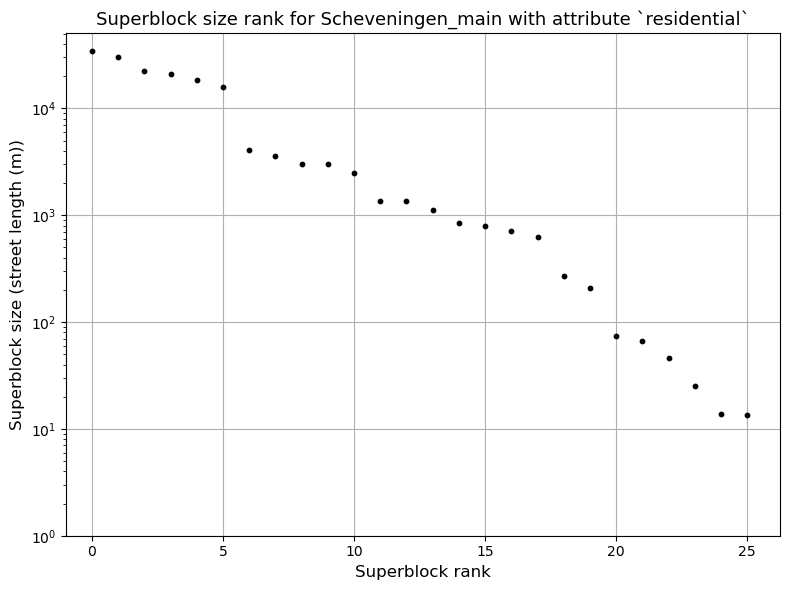
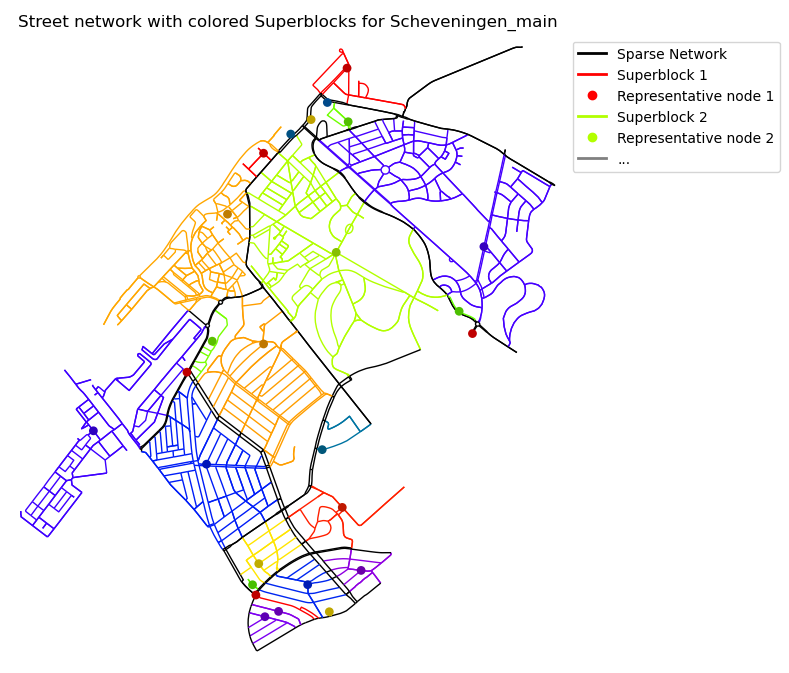
The partitioner has been run and for each Superblock it produces a partition, inclusing a subgraph object, which includes the nodes and edges of the Superblock. One of them looks like this:
subgraph = part.partitions[6]["subgraph"]
subgraph_edges = ox.graph_to_gdfs(subgraph, nodes=False, edges=True)
subgraph_edges.explore(style_kwds={"weight": 4})
As edges are represented by linestrings, the area is not clearly defined. The first idea that might come to one’s mind is the convex hull of the linestrings.
# From subgraph_edges we want to get a hull that encloses all edges
convex_hull = subgraph_edges.union_all().convex_hull
# Make gdf from convex hull with the same crs as the subgraph
convex_hull_gdf = gpd.GeoDataFrame(
geometry=[convex_hull], crs=subgraph_edges.crs
)
# plot both gdfs together
ax = subgraph_edges.plot()
convex_hull_gdf.plot(ax=ax, color="lightgray")
plt.axis("off")
plt.show()
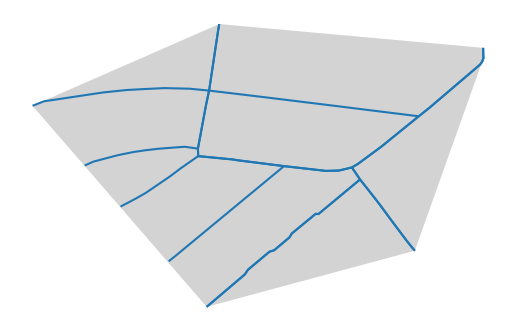
This approach is quick and easy, but it has some drawbacks. It might be larger than
we are looking for. For example, a star shaped neighborhood would result in a hull
spanning around all areas between the streets, even if it might include areas that
belong to another Superblock. Also, it might be smaller than we are looking for. For example,
a neighborhood that is linear, one long street with houses on both sides, would result
in a hull that is just a line, which is not what we are looking for.
The latter problem can be solved by buffering the edges before taking the convex hull.
The former problem has multiple solutions summarized under the term concave hull.
shapely provides the function
concave_hull for this purpose. It takes a ratio
parameter, which determines how concave the hull is. A ratio of 1 results in the convex
hull, a ratio of 0 results in only a line between the nearest points in the geometry.
Show code cell source
from numpy import linspace
def plot_concave_hull(ax, subgraph_edges, ratio=0.4, allow_holes=False,
color="crimson"):
concave_hull = shp.concave_hull(
subgraph_edges.union_all(),
ratio=ratio,
allow_holes=allow_holes,
)
# Make gdf from convex hull with the same crs as the subgraph
convex_hull_gdf = gpd.GeoDataFrame(
geometry=[concave_hull], crs=subgraph_edges.crs
)
# plot both gdfs together
convex_hull_gdf.plot(ax=ax, color=color)
# Figure different ratios
fig = plt.figure(layout="constrained", figsize=(10, 8))
subfigs = fig.subfigures(2, 1, hspace=0.07, height_ratios=[2., 1.])
# Overlaying
axs0 = subfigs[0].subplots(1, 1)
for ratio in linspace(1, 1/10, 10):
color = plt.cm.coolwarm(ratio)
plot_concave_hull(axs0, subgraph_edges, ratio=ratio, color=color)
subgraph_edges.plot(ax=axs0, color="black", linewidth=3)
axs0.set_axis_off()
colorbar = plt.cm.ScalarMappable(cmap=plt.cm.coolwarm,
norm=plt.Normalize(vmin=1, vmax=0.1))
# vertically oriented colorbar with title Ratio of Alpha Shape
cbar = fig.colorbar(colorbar, ax=axs0, orientation="vertical", shrink=0.8)
cbar.set_label("Ratio of Alpha Shape", rotation=270, labelpad=20)
cbar.ax.get_yaxis().labelpad = 20
# Side by side
axs1 = subfigs[1].subplots(1, 7)
for i, ratio in enumerate(linspace(1, 1/10, 7)):
color = plt.cm.coolwarm(ratio)
plot_concave_hull(axs1[i], subgraph_edges, ratio=ratio, color=color)
subgraph_edges.plot(ax=axs1[i], color="black", linewidth=3)
axs1[i].set_axis_off()
plt.show()
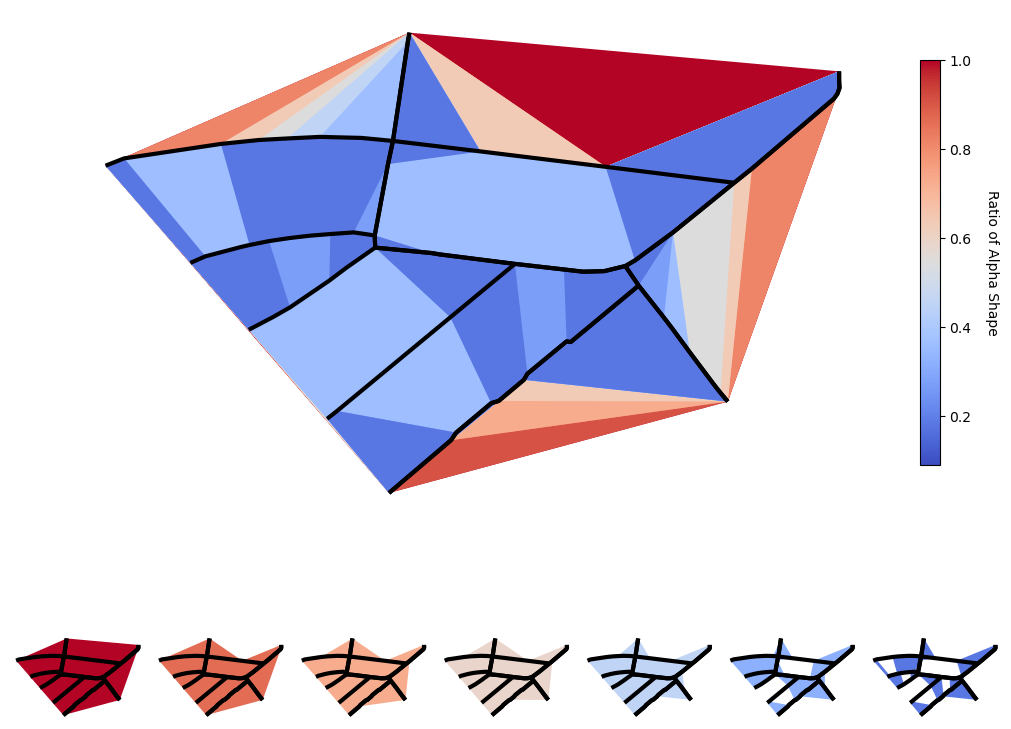
The function works with the points in the linestrings, so it is highly dependent on the point density. The ratio determines the maximum edge length, rescaled between the greatest and smallest distance between al pairs of points. This results in the fact, that a shape with lower ratio is not necessarily fully included in a shape with a higher ratio, see the two lowest ratios on the bottom right. This solution still does not satisfy us.
Optimally all Superblock cells would not overlap each other and form a tiling, also called tesselation, of the city.
Morphological Tessellation#
There is a solution satisfying our requirements. Okabe and Sugihara define the
line Network Voronoi Diagram (line N-VD) [Equation 4.7]. It is basically a Voronoi
diagram (also called Thiessen polygons in some fields) where lines are made up of
multiple points[1].
Araldi and Fusco use this idea to do geostatistical analysis[2]. Fleischmann et al.
implement the same idea in the momepy package for building footprints [3].
With list of footprint geometries, the Tessellation
class returns a GeoDataFrame with a cell corresponding to each input geometry that was
given.

In our case the input geometries can be the smaller neighborhood boundaries, and the tesselation fills up the gaps. For the Superblocks we will use an union of the edges of the subgraphs and buffer them a small bit. As we do not want the polygons to overlap wich each other, we’ll buffer using a flat cap style.
def border_from_subgraph_shrinked(subgraph, buffer=1):
"""Shrinked subgraph borders, to avoid overlap between partitions.
Does work well with small buffer values."""
edges = ox.graph_to_gdfs(subgraph, nodes=False, edges=True)
# First buffer with flat cap style to avoid self-intersections
polygon = shp.Polygon(edges.union_all().buffer(2 * buffer, cap_style='flat')
.exterior)
# Simplify the polygon to remove small artifacts of flat cap style at curved edges
# polygon = polygon.simplify(buffer*2, preserve_topology=True)
# geos::simplify::PolygonHullSimplifier would do the job. No bindings yet.
# https://libgeos.org/doxygen/classgeos_1_1simplify_1_1PolygonHullSimplifier.html
# http://lin-ear-th-inking.blogspot.com/2022/04/outer-and-inner-concave-polygon-hulls.html
# http://lin-ear-th-inking.blogspot.com/2022/05/using-outer-hulls-for-smoothing.html
# Secondly, erode the polygon to avoid overlap between partitions
return polygon.buffer(-buffer, cap_style='round')
border_from_subgraph_shrinked(part.partitions[6]["subgraph"], buffer=1)
We would like to simplify the polygon before buffering down, but as we use a flat
cap style, the line connection have small artifacts when choosing larger buffers.
The Ramer–Douglas–Peucker algorithm does not suffice our needs, because the result can
split the polygon up and does not inherently enclose the original polygon.
The geos::simplify::PolygonHullSimplifier would do the job, but it got added in GEOS
3.11, and no python package has any bindings, yet.
Now, when using the momepy.Tessellation class, we get:
from momepy import Tessellation
borders = gpd.GeoDataFrame(
geometry=[border_from_subgraph_shrinked(p["subgraph"], buffer=1) for p in part
.partitions],
crs=part.partitions[0]["subgraph"].graph["crs"],
data=[p["name"] for p in part.partitions],
columns=["partition_id"]
)
# Morphological tessellation around given buildings ``gdf`` within set ``limit``.
tessellation = Tessellation(borders, unique_id="partition_id",
limit=part.graph.graph["boundary"],
shrink=0.0)
# Plot on our map
tessellation_gdf = tessellation.tessellation
fig, axe = plt.subplots(figsize=(10, 10))
tessellation_gdf.plot(ax=axe, edgecolor="white", column="partition_id", legend=True,
cmap="tab20")
borders.plot(ax=axe, color="white", alpha=0.5, facecolor="white")
ox.plot_graph(part.sparsified, ax=axe, node_size=0, edge_color="black",
edge_linewidth=1)
axe.set_axis_off()
plt.show()
/home/runner/micromamba/envs/sb_env/lib/python3.12/site-packages/tqdm/auto.py:21: TqdmWarning: IProgress not found. Please update jupyter and ipywidgets. See https://ipywidgets.readthedocs.io/en/stable/user_install.html
from .autonotebook import tqdm as notebook_tqdm
/tmp/ipykernel_2561/1210318133.py:11: FutureWarning: Class based API like `momepy.Tessellation` is deprecated. Replace it with `momepy.morphological_tessellation` or `momepy.enclosed_tessellation` to use functional API instead or pin momepy version <1.0. Class-based API will be removed in 1.0.
tessellation = Tessellation(borders, unique_id="partition_id",
Generating input point array...
Generating Voronoi diagram...
Generating GeoDataFrame...
Dissolving Voronoi polygons...
/tmp/ipykernel_2561/1210318133.py:11: UserWarning: Tessellation contains MultiPolygon elements. Initial objects should be edited. `unique_id` of affected elements: ['residential_10', 'residential_15'].
tessellation = Tessellation(borders, unique_id="partition_id",
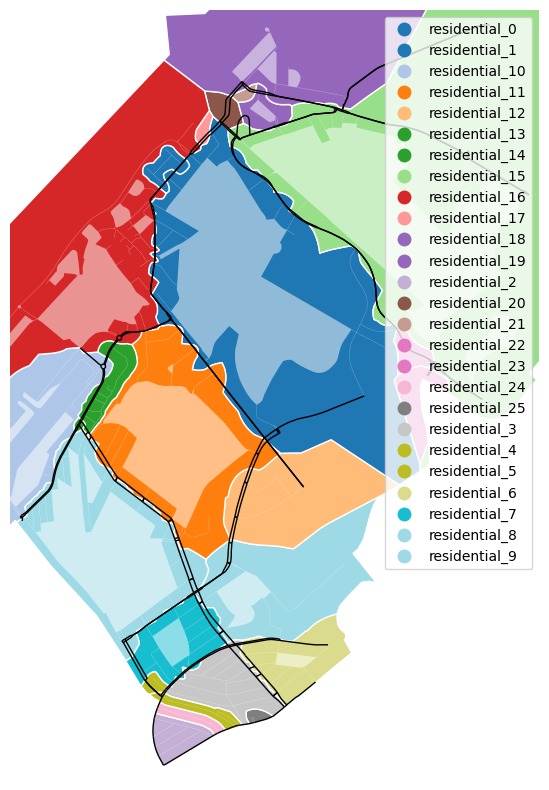
This is much more what we want. Another way to make it even better it so take the sparsified network at cell borders, but at the same time, the sparsified network should also have a volume as there might be people living on it. Finally, we will implement our own method, inspired by this technique, a solution sewed to our needs.
Independent Tessellation#
When looking into the code, momepy uses scipy.spatial.Voronoi
to generate the tessellation for every enclosure. This is done with a dense point array
for the geometry boundaries (borders in our case).
As we want to calculate area and population for each Partition, we can save time by
calculating the Voronoi diagram once for the whole graph/city, and save area and
population for each edge. Later we can use this data to calculate the area and
population for each Partition.
Show code cell source
import pandas as pd
import numpy as np
from scipy.spatial import Voronoi, voronoi_plot_2d
Now, we will create Voronoi cells for each edge, so we can later dissolve them to
Superblock cells. As we are working in a MultiDiGraph two way streets are represented by two
directed edges with the same geometry, both should share the same cell, so grouping the
edges is a crucial part. First we will group the edges connecting the same nodes u and
v and then we will merge the edges with the same or reverse geometry.
edges = ox.graph_to_gdfs(part.graph,
nodes=False,
edges=True,
node_geometry=False,
fill_edge_geometry=True)
# `edges` is a pandas dataframe with the multiindex (u, v, key)
# Merge two columns, when the geometry of one is equal or the reverse of the other
# 1. Group if u==u and v==v or u==v and v==u (match for hashed index (u, v) where u<v)
# get flat index of the first match
edges["edge_id"] = edges.index.to_flat_index()
# sort the edge_id tuples
edges["node_pair"] = edges["edge_id"].apply(lambda x: tuple(sorted(x[:2])))
# 2. Aggregate if the geometry is equal or the reverse of the other
# Merge columns if geometry_1 == geometry_2 or geometry_1 == geometry_2.reverse()
# reverse geometry if x_start >= x_end
edges["geometry"] = edges["geometry"].apply(
lambda x: x if x.coords[0] < x.coords[-1] else x.reverse())
# 3. Group by node_pair and geometry
edges = edges.groupby(["node_pair", "geometry"]).agg({
"edge_id": tuple,
"component_name": "first",
}).reset_index()
edges.set_index("edge_id", inplace=True)
edges = gpd.GeoDataFrame(edges, geometry="geometry", crs=part.graph.graph["crs"])
edges.explore()
For each geometry we will interpolate the lines into points of equal distance of 10m.
# get multiindex of first row
distance = 10
# The maximum distance between points after discretization.
edge_points = []
edge_indices = []
# iterate over street_id, geometry
for idx, geometry in edges["geometry"].items():
if geometry.length < 2 * distance:
# for edges that would result in no point, take the middle
pts = [shp.line_interpolate_point(geometry, 0.5, normalized=True)]
else:
# interpolate points along the line with at least distance between them
# start and end 0.1 from the ends to avoid edge effects
pts = shp.line_interpolate_point(
geometry,
np.linspace(
0.1,
geometry.length - 0.1,
num=int((geometry.length - 0.1) // distance),
),
) # offset to keep nodes out
edge_points.append(shp.get_coordinates(pts))
# Append multiindices for this geometry
edge_indices += [idx] * len(pts)
points = np.vstack(edge_points)
Now we know for each point, which edge it belongs to. We can use this to calculate the Voronoi diagram.
Before we continue, let’s also introduce a hull around the points, so that the outer edge cells are not infinite or too large. As a hull we can use the boundary polygon of the graph from OSM, as used in the node approach, or a buffered union of the edge geometries. Then we can also split up the hull into points and add them to the points array.
hull = shp.Polygon(edges.union_all().buffer(100).exterior)
# interpolate points along the hull - double the distance
hull_points = shp.line_interpolate_point(
hull.boundary,
np.linspace(0.1, hull.length - 0.1, num=int(hull.length // (2 * distance))),
)
# add hull points to the points array
points = np.vstack([points, shp.get_coordinates(hull_points)])
# add edge indices to the edge_indices array
edge_indices += [-1] * len(hull_points)
For the points array we can now calculate the Voronoi diagram.
edge_voronoi_diagram = Voronoi(points)
Show code cell source
from matplotlib.patches import Rectangle, ConnectionPatch
# Plot with inset axes
fig, axe = plt.subplots(figsize=(10, 10))
zoom_window = (587000, 587500, 5772000, 5772500)
edges.plot(ax=axe, color="black", linewidth=0.5)
voronoi_plot_2d(edge_voronoi_diagram, ax=axe, show_vertices=False, line_colors='orange',
line_width=1, line_alpha=0.6, point_size=2)
axe.set_title("Voronoi diagram of dense edge points")
# Create inset axes
axins = axe.inset_axes([0.6, 0.01, 0.45, 0.45])
edges.plot(ax=axins, color="black", linewidth=2)
voronoi_plot_2d(edge_voronoi_diagram, ax=axins, show_vertices=False,
line_colors='orange',
line_width=2, line_alpha=0.6, point_size=4)
axins.set_xlim(*zoom_window[:2])
axins.set_ylim(*zoom_window[2:])
axins.set_xticks([])
axins.set_yticks([])
# Indicate zoom window
rect = Rectangle((zoom_window[0], zoom_window[2]), zoom_window[1] - zoom_window[0],
zoom_window[3] - zoom_window[2], linewidth=1, edgecolor='r',
facecolor='none', zorder=10)
axe.add_patch(rect)
# Connect zoom window to inset
axe.add_artist(
ConnectionPatch(xyA=(zoom_window[0], zoom_window[2]),
xyB=(zoom_window[0], zoom_window[2]),
coordsA="data", coordsB="data", axesA=axe, axesB=axins,
linewidth=1, zorder=10))
axe.add_artist(
ConnectionPatch(xyA=(zoom_window[1], zoom_window[3]),
xyB=(zoom_window[1], zoom_window[3]),
coordsA="data", coordsB="data", axesA=axe, axesB=axins,
linewidth=1, zorder=10))
plt.show()
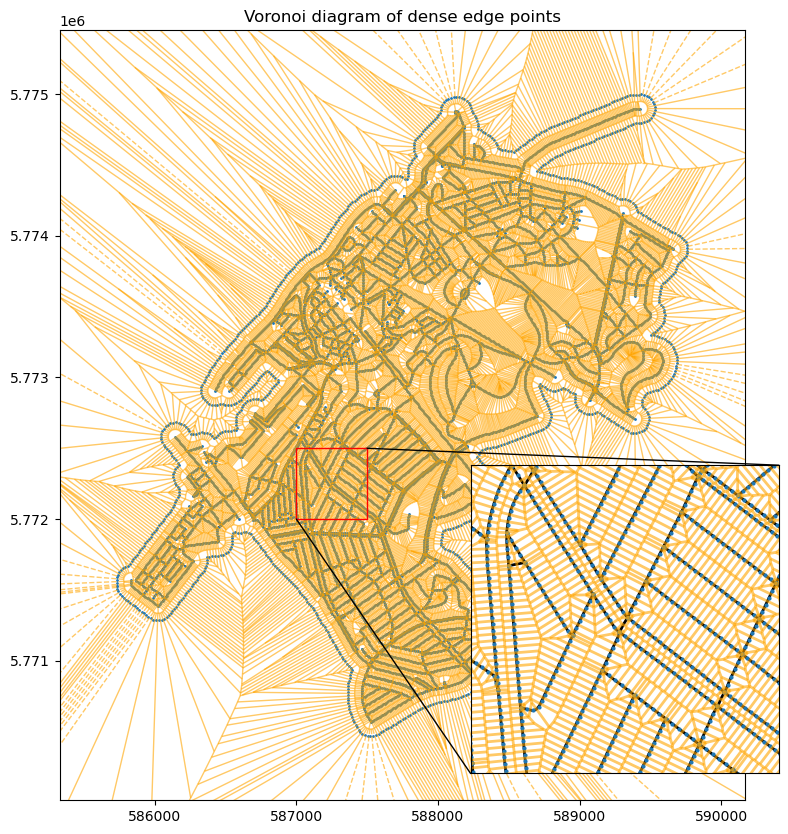
Let’s see how the cells look like for the Partitioner part.
# Construct cell polygons for each of the dense points
point_vertices = pd.Series(edge_voronoi_diagram.regions).take(
edge_voronoi_diagram.point_region)
point_polygons = []
for region in point_vertices:
if -1 not in region:
point_polygons.append(
shp.polygons(edge_voronoi_diagram.vertices[region]))
else:
point_polygons.append(None)
# Create GeoDataFrame with cells and index
edge_poly_gdf = gpd.GeoDataFrame(
geometry=point_polygons,
index=edge_indices,
crs=part.graph.graph["boundary_crs"],
)
# Drop cells that are outside the boundary
edge_poly_gdf = edge_poly_gdf.loc[edge_poly_gdf.index != -1]
# Dissolve cells by index
edge_poly_gdf = edge_poly_gdf.dissolve(by=edge_poly_gdf.index)
# delete index_str
edge_poly_gdf
| geometry | |
|---|---|
| ((27372680, 1428324110, 0), (1428324110, 27372680, 0)) | POLYGON ((587436.747 5773992.7, 587432.451 577... |
| ((27457350, 27458481, 0), (27458481, 27457350, 0)) | POLYGON ((587682.119 5773570.263, 587666.386 5... |
| ((27457350, 45266004, 0), (45266004, 27457350, 0)) | POLYGON ((587694.731 5773558.934, 587682.872 5... |
| ((27457350, 45268282, 0), (45268282, 27457350, 0)) | POLYGON ((587695.119 5773574.589, 587694.204 5... |
| ((27458481, 45269635, 0),) | POLYGON ((587667.009 5773624.551, 587663.329 5... |
| ... | ... |
| ((282316119962854798872503583622236536634, 3790141190, 1),) | POLYGON ((588051.115 5770814.969, 588040.511 5... |
| ((286957140641811869917340023700264958761, 10805243558, 0),) | POLYGON ((587912.356 5774381.673, 587916.168 5... |
| ((286957140641811869917340023700264958761, 10805243559, 0),) | POLYGON ((587912.356 5774381.673, 587916.168 5... |
| ((296388111720839557739481376725235382839, 45293864, 0),) | POLYGON ((587756.953 5774262.325, 587778.161 5... |
| ((296388111720839557739481376725235382839, 1427521880, 0),) | POLYGON ((587756.953 5774262.325, 587778.161 5... |
1559 rows × 1 columns
The GeoDataFrame now includes the cell geometries for each edge tuple.
edge_poly_gdf["component_name"] = edges.loc[edge_poly_gdf.index, "component_name"]
# Set NaNs to "sparse"
edge_poly_gdf["component_name"] = edge_poly_gdf["component_name"].fillna("sparse")
# Plot with color by edge label
fig, axe = plt.subplots(figsize=(10, 10))
edge_poly_gdf.plot(column="component_name", ax=axe, legend=True, cmap="tab20")
ox.plot_graph(part.graph, ax=axe, node_size=8, edge_color="black", edge_linewidth=0.5,
node_color="black")
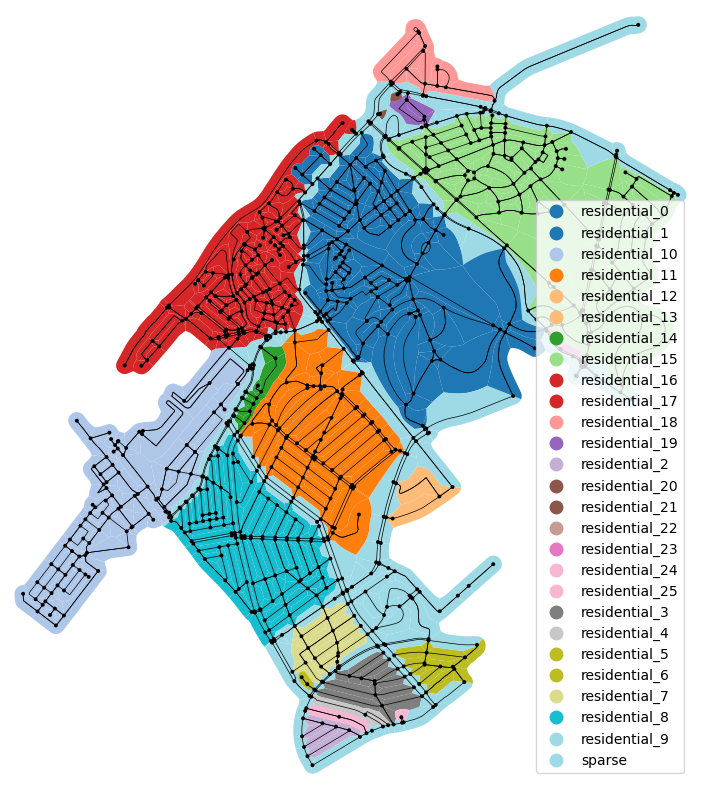
(<Figure size 1000x1000 with 1 Axes>, <Axes: >)
When dissolving the cells grouped by the component_name we get the wanted regions.
# Interactive explore map with unions of partitions
edge_poly_gdf.dissolve(by="component_name", as_index=False).explore(
column="component_name", cmap="tab20")
Implementation#
We implemented a function that does this and more for us in one function call.
add_edge_cells accepts a graph and adds a cell attribute with the
cell geometry to every edge.
ky_graph = ox.graph_from_place("Kyiv, Ukraine", network_type="drive")
ky_graph = ox.project_graph(ky_graph)
For a graph as big as Kyiv, 7th largest European city as of 1st of January 2021, this takes about a minute. This graph has more than 23k edges, resulting in about 300k points for the Voronoi diagram (10m interpolation) ans 13k edge cells.
sb.add_edge_cells(ky_graph)
2024-12-04 10:43:08,394 | INFO | tessellation.py:101 | Calculating edge cells for graph with 23314 edges.
2024-12-04 10:43:54,215 | INFO | tessellation.py:155 | Tessellated 14076 edge cells in 0:00:45.
Show code cell source
# Get polygons from edges and plot
edge_poly_gdf = gpd.GeoDataFrame(
geometry=[data["cell"] for _, _, data in ky_graph.edges(data=True)],
crs=ky_graph.graph["crs"],
index=ky_graph.edges(),
columns=["geometry"],
)
fig, axe = plt.subplots(figsize=(10, 10))
edge_poly_gdf.plot(ax=axe, color="orange", alpha=0.5, edgecolor="black", linewidth=0.5)
ox.plot_graph(ky_graph, ax=axe, node_size=0, edge_color="black", edge_linewidth=0.5,
node_color="black")
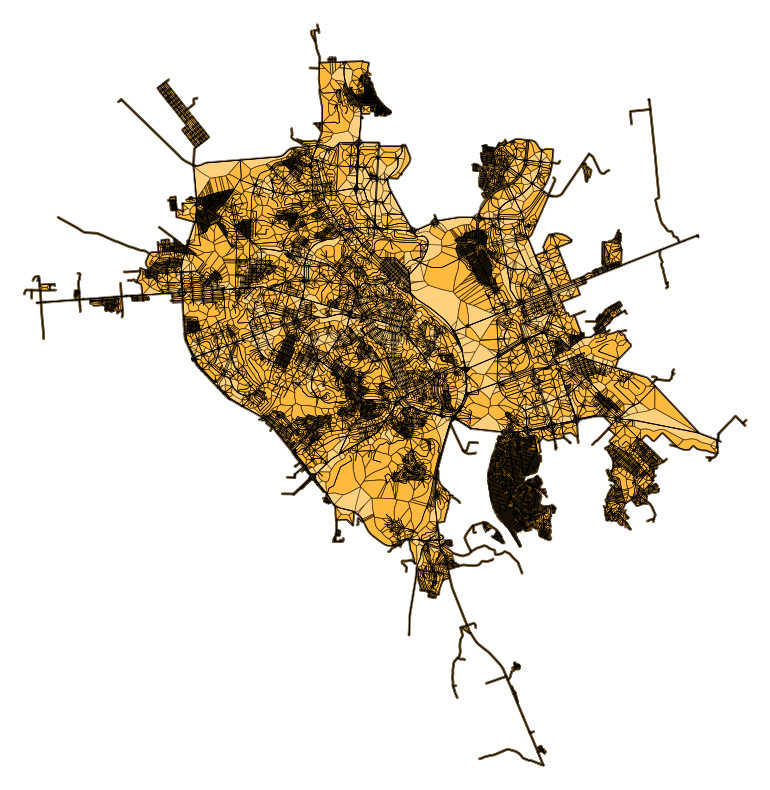
(<Figure size 1000x1000 with 1 Axes>, <Axes: >)
- superblockify.population.tessellation.add_edge_cells(graph, **tess_kwargs)[source]
Add edge tessellation cells to edge attributes in the graph.
Tessellates the graph into plane using a Voronoi cell approach. Function writes to edge attribute cells of the graph in-place. Furthermore, cell_id is added to the edge attributes, for easier summary of statistics later.
The approach was developed inspired by the
momepy.Tessellationclass and tessellates withscipy.spatial.Voronoi.- Parameters:
- graphnetworkx.MultiDiGraph
The graph to tessellate.
- **tess_kwargs
Keyword arguments for the
superblockify.population.tessellation.get_edge_cells()function.
- Raises:
- ValueError
If the graph is not in a projected coordinate system.
- ValueError
If the limit and the edge points are disjoint.
Notes
The graph must be in a projected coordinate system.

